La projection

Projection d'un point sur une droite parallèlement à une autre droite

Soient deux droites sécantes (D₁) et (D₂), un point A. Construire le projeté de A sur (D₂) parallèle à (D₁)

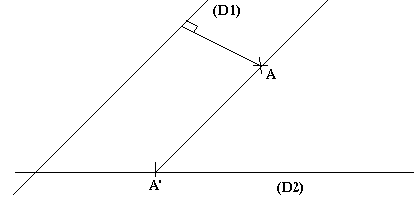
Construire une parallèle à (D₁) passant par le point A.
Le point d'intersection de la parallèle aussi construite avec (D₂) s'appelle le projeté de A sur (D₂)

Propriété d'un segment [AB] sur (D₂) parallèle à (D₁)

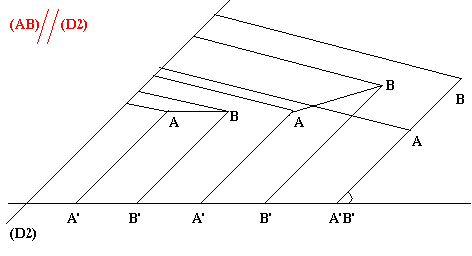
Le projeté de [AB] est [A'B'] et AB=A'B'
Le projeté de [CD] est [C'D'] CD=C'D'
[EF] est [E'F']; EF=E'F'

Théorème des milieux

Dans un triangle, la droite qui relie les milieux de deux côtés est parallèle à son troisième côté.
Dans un triangle, le segment qui a pour extrémités les milieux de deux côtés de ce triangle a une longueur égale à la moitié de la longueur du troisième côté du triangle.

Exercice d'application:

Construisez un triangle quelconque ABC.
Soit I le milieu de [AC] et J el milieu de [AB], construisez le point K symétrique de I par rapport à J.

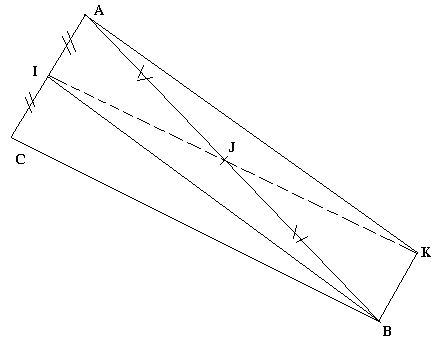
C'est un parallélogramme parce que ses diagonales [AB] et [IK] se coupent en leur milieu J. Quelles sont les positions relatives des droites (AI) et (KB), elles sont parallèles car elles sont des supports des côtés du parallélogramme AIBK. Comparez les longueurs AI et BK. AI#BK en AI=IC=BK. On a (IA)=(IC) or (IA) parallèle à (BK) donc (IC) est parallèle à (BK) compte tenu de ce que BK=IC et (BK) parallèle à (IC). On en déduit que ICBK est un parallélogramme. Nous savons que IJ=BK/2 et que IK=CB donc IJ=CB/2.

Réciproque du premier théorème des milieux

Dans un triangle, la droite qui passe par le milieu d'un côté et qui est parallèle au deuxième côté coupe le troisième milieu.