Produit scalaire - Propriétés du produit scalaire

Propriétés du produit scalaire

Vecteurs orthogonaux

Propriété:

Pour tout vecteur u et v on a:
u.v=0

Conséquence de la propriété

Règles de calcul

Pour tous vecteur u, v, u', v' et tout nombre réel λ on a:

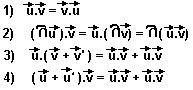
Autre expression du produit scalaire

Pour tout vecteur u et v on a:

Relation métrique dans un triangle

Relation métrique caractérisant un triangle rectangle

On sait que si le triangle ABC est rectangle en A alors BC²=AB²+AC² (théorème de Pythagore).
Soit ABC un triangle, H est le projeté orthogonal de A sur (BC). Les énoncés suivants sont équivalents

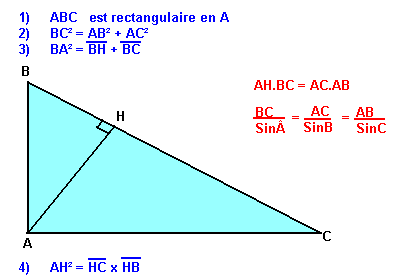
Théorème d'AKASHI;

Soit ABC un triangle quelconque.

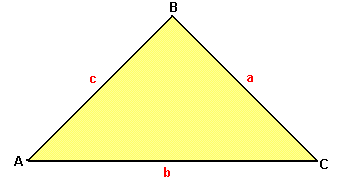
On pose a=BC ; b=AC ; c=AB
On a: a² = b² + c² - 2bcCosÂ

Forme analytique du produit scalaire

Expression dans une base orthonormée

Conséquence