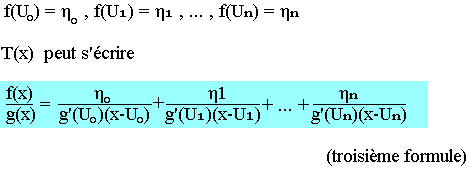Calcul des limites

Principaux développement en série entière de fonction classiques: au voisinage de x₀=0

x→e^x = 1 + x/1! + x²/2! + x³/3! + ... + x^K/K! + ...

x→Cos(x) = 1 - x²/2! + x⁴/4! - x⁶/6! + ... + (-1)^px^2p/2p! + ...
x→Sin(x) = x - x³/3! + x⁵/5! - x⁷/7! + ... + (-1)^p+1x^2p+1/(2P+1)! + ...

x→Ch(x) = 1 + x²/2! + x⁴/4! + x⁶/6! + ... + x^2P/2P! + ...
x-→Sh(x) = x + x³/3! + x⁵/5! + x⁷/7! + ... + (-1)^P+1x^2P+1/(2P+1)! + ...

Ln(1+x) = x - x²/2 + x³/3 - x⁴/4 + ... + (-1)^P+1x^P/P + ...
Arct(x) = x - x³/3 + x⁵/5 - x⁷/7 + ... + (-1)^P+1x^2P+1/(2P+1) + ...

Valeur approchées à 10^-P près

Formule d'interpolation

Interpolation d'équation simple

Soient y₀, y₁, y₂, ... y_n les valeurs prises par une certaines fonctions y=f(x) lorsque x prend les valeurs respectives x₀, x₁, x₂, ... x_n équidistantes.
x₁-x₀=x₂-x₁=...=x_n-x_n-1=H constante
de plus y₁-y₀=D₀; Y₂-Y₁=D₁...; y_n-y_n-1=D_n-1
Alors si y et x sont tels que (x_i<x<x_i+1) et (y_i<y<y_i+1) on montre que:

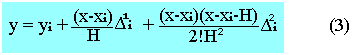
Démonstration:

Donnons l'expression complète de y₀, y₁, ..., y_n en fonction de D_i
D₀=y₁-y₀; D₀²=D₁-D₀=(y₂-y₁)-(y₁-y₀)=y₂-2y₁+y₀
Remplaçons y₂ et y₀ par leur expression en fonction de y₀
D₁-D₀=y₂-2(y₀+D₀)+y₀
D₁-D₀=y₂-y₀-2D₀
y₂=(D₁-D₀)+y₀2D₀
y₂=D₀²+y₀+2D₀ (1)

Ecrivons x₁, x₂, ..., x_n eb fonction de H
x₁-x₀=H ; x₁=x₀+H
x₂-x₀=2H ; x₂=x₀+2H
x_n-x₀=nH ; x_n=x₀+nH
(2) H=x₁-x₀=(x₂-x₀)/2=...=(x_n-x₀)/n Sachant que 2=(x₂-x₀)/H
(1) devient Y₂=D₀² + y₀ + D₀(x₀-x₀)/H or d'après (2)
2=(x₂-x₀)/H ; 1=(x₂-x₀)/2H
de même x₁=x₂-H et 1=(x₁-x₀)/H et on a:
y₂ = y₀ + (x₂-x₀D₀/H + (x₂-x₀)(x₂-x₀-H)D₀²/2H²

Polynôme d'Interpolation de Lagrange

Etant donné (n+1) couple (a₀,;b₀), (a₁,b₁), ... (_n,b_n) tel que b₀=f(a₀), b₁=f(a₁),...b_n=f(a_n)
On désire trouver un polynôme P_k de degré k qui vérifie (E).
Le mathématicien Lagrange a montré qu'un tel polynôme existe et que k=n

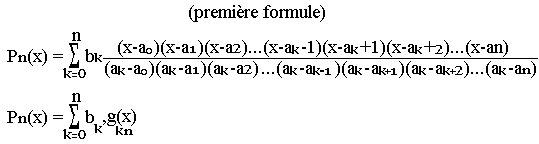
Exercice:

Soit les couples A(0,2); B(-1,2) et C(1,4) déterminez le polynôme de Lagrange dont la courbe passe par A, B et C

Solution:

a₀=0 ; b₀=2
a₁=1 ; b₁=2
a₂=1 ; b₂=4
b₀(x-a₁)(x-a₂)/(a₀-a₁)(a₀-a₂) + b₁(x-a₀)(x-a₂)/(a₁-a₀)(a₁-a₂)
P₂(x) = x² + x + 2
P(0) = 2
P(-1) = 2
P(1) = 4

Polynôme de Lagrange: cas des fractions rationnelles

Soit T(x)=f(x)/g(x) avec degré f(x) < degré g(x)
Alors U₀, U₁, U₂, ..., U_n sont des racines simples de g(x) et si de plus