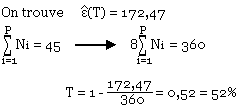Page 2 sur 3
Théorème de l'entropie
Exemple
Soit le texte en clair "Le_codage_des_informations_utilise_du_binaire"
- Classer par ordre d'apparition chaque caractère du texte
- Déterminez l'entropie de chaque caractère.
Solution
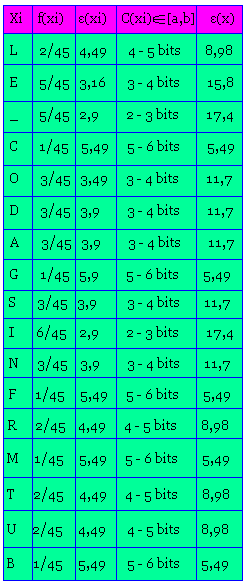
Classons par ordre d'apparition chaque caractère du texte.
|
L |
E |
_ |
C |
O |
D |
A |
G |
S |
I |
N |
F |
R |
M |
T |
U |
B |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||||
|
1 |
1 |
1 |
||||||||||||||
|
1 |
1 |
1 |
||||||||||||||
|
1 |
1 |
Taille totale (en décimal): 45
Donnons l'entropie de chaque caractère:
Entropie totale:
Soit (T) un texte en claire utilisant P caractères (X1, X2, X3,... XP) d'occurrence respective n1, n2, n3, ... nP alors l'entropie totale du texte (nombre total de digits qu'occupera le texte après compression).
Taux moyen de compression
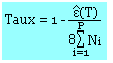
Application:
- Déterminez le taux de compression de l'exercice précédent
- Déterminez les codes de chacun des caractères (ressortir l'arbre pour sortir les codes)
Solution:
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale