Transformée de Fourrier à cosinus (TFC) et à sinus (TFS)

Si f est une fonction transformable en série de Fourrier sur:

Transformée et parité de f

Si f est une fonction vérifiant la condition (C₁) alors:

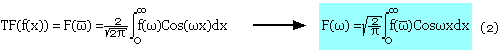
Si f vérifie (c₁) et f impaire on aura:

Transformée en cosinus et en sinus

Les équations (2) et (3) précédents sont intéressantes, surtout lorsqu’il s'agit de convertir un signal temporel en un spectre fréquentiel. C'est pourquoi elles ont été utilisées même pour des fonctions ni paires ni impaires. On définit alors les transformée de Fourier en cosinus (TFC) et les transformées de Fourrier en sinus (TFS).

TFC/TFS

Si une fonction vérifie (c₁) sur un intervalle [a, b], alors ses transformées en cosinus et en sinus existent et sont définies par:

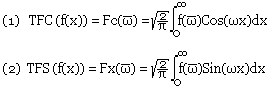
Exercice

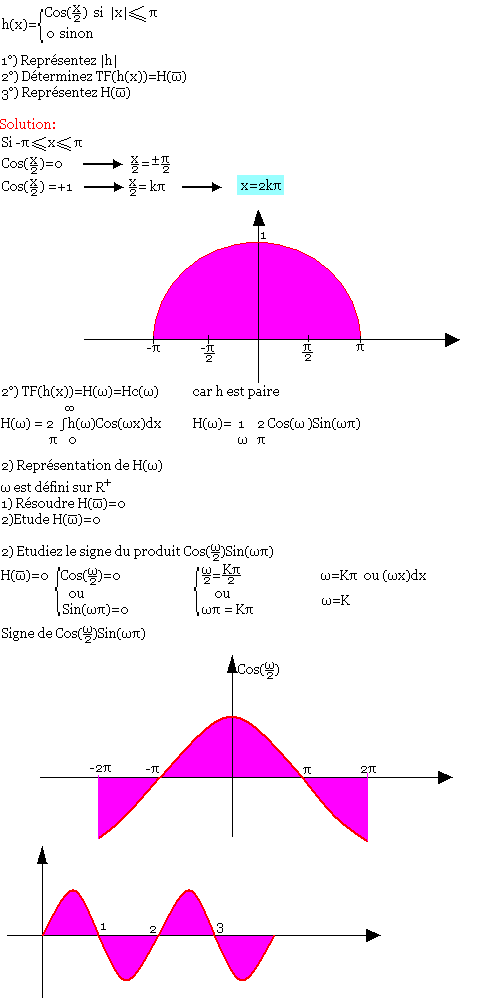
Soit la fonction h définie par: