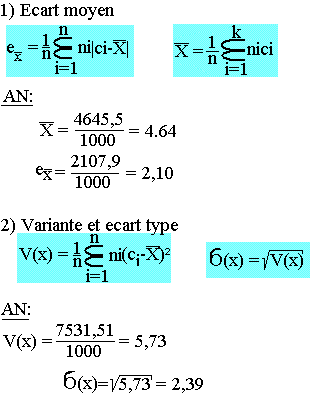Comme caractéristique de position on a le mode, la moyenne, la médiane.
Le mode
On appelle mode la valeur du caractère ayant le plus grand effectif
Exemple 1:
Cas d'un caractère discret
Déterminez le mode de la série statistique suivante
|
Modalité (xi) |
0 |
1 |
2 |
3 |
4 |
|
Effectif (ni) |
3 |
8 |
16 |
7 |
6 |
Le plus grand effectif est 16, alors le mode M0=2
Exemple 2:
Cas d'un caractère continue
Déterminer le mode de la série statistique suivante
|
xi |
[5; 10[ |
[10; 15[ |
[15; 20[ |
[20; 25[ |
[25; 30[ |
|
ni |
2 |
3 |
7 |
10 |
5 |
Le plus grand effectif est 10 alors [20; 25[est la classe modale, c'est-à-dire les valeurs comprises entre 20 et 25 représentent toutes le mode.
La moyenne
Exemple 1: Cas d'un caractère direct
Pour une série statistique (xi, ni) le moyenne
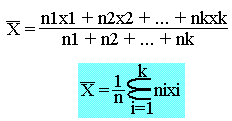
Calculez la moyenne arithmétique de la série statistique suivante
|
xi |
2 |
5 |
7 |
8 |
9 |
10 |
11 |
12 |
Total |
|
ni |
1 |
2 |
3 |
4 |
4 |
7 |
7 |
9 |
37 |
|
nixi |
2 |
10 |
21 |
32 |
36 |
70 |
77 |
108 |
256 |
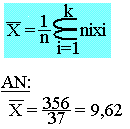
Exemple 2:
Cas d'un caractère continu
La moyenne d'une série statistique pour un caractère continu est la moyenne de la série (ci, ni)
ci: étant le centre de la classe
Pour une classe [a; b[ Ci1/2= (a+b)
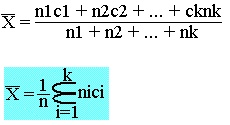
Déterminer la moyenne de la série suivante
|
xi |
[10; 20[ |
[20; 25[ |
[25; 40[ |
[40; 45[ |
[45; 50[ |
Total |
|
ni |
60 |
45 |
90 |
40 |
15 |
250 |
|
Ci |
15 |
22,5 |
32,5 |
42,5 |
47,5 |
|
|
niCi |
900 |
1012,5 |
2925 |
1700 |
712,5 |
7250 |
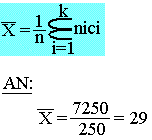
La médiane (Me)
La médiane d'une série statistique est la valeur de la variable qui partage en 2 effectifs égaux les individus d'une population statistique supposée rangée par ordre de grandeur croissante ou décroissante.
Cas des observations non groupées
Série impaire
Exemple:
Soit la série 3; 5; 7; 9; 11; 13; 15
Me=9
Série paire
Exemple:
3; 5; 7; 9; 11; 13. On parle ici d'intervalle médiane c'est-à-dire Me appartient à [7; 9]
Cas des observations groupées
La médiane s'obtient ici par interpolation linéaire
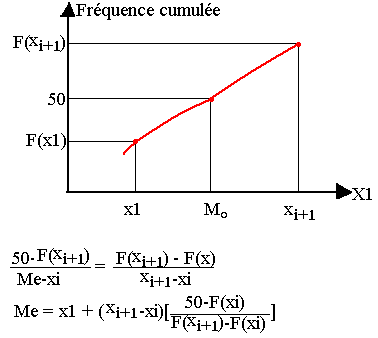
þi(%)=100*ni/n
Exemple:
Déterminez la médiane de série statistique suivante
|
xi |
[10; 20[ |
[20; 25[ |
[25; 40[ |
[40; 45[ |
[45; 50[ |
[50; 60[ |
Total |
|
ni |
60 |
45 |
90 |
40 |
15 |
50 |
300 |
|
fi(%) |
20 |
15 |
30 |
13 |
5 |
17 |
100 |
|
Fi(%) |
20 |
35 |
65 |
78 |
83 |
100 |
M2 est la médiane ici parce que 35 et 65 est compris en 50% c'est-à-dire 50 appartient à 35 et 65
La classe médiane est [25; 40[et 25<Me<40
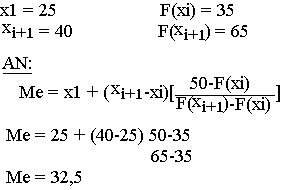
Les caractéristiques de dispresion
Une caractéristique de dispersion est un nombre qui permet de connaître la répartition des individus au tour de la moyenne. On distingue:
- L'écart moyen
- La variance
- L'écart type
L'écart moyen
C'est la moyenne des écarts à la moyenne
- Pour le cas d'une statistique discrète
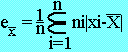
- Pour le cas d'une variable statistique continue (observation groupée)
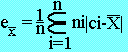
La variation et l'écart type
- La variation est la moyenne des carrés des écarts à la moyenne.
- Pour une variation statistique discrète
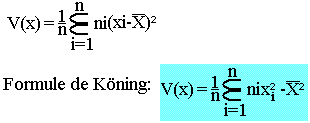
- Pour une variable statistique continue
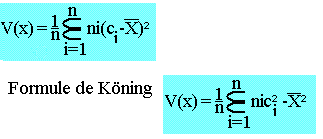
- L'écart type est la racine carrée de la variance
![]()
Exemple:
On considère la série statistique présentée dans le tableau suivant
|
Classe (xi) |
[1; 2[ |
[2; 4[ |
[4; 5[ |
[5; 6[ |
[6; 9[ |
|
Effectif (ni) |
258 |
133 |
164 |
108 |
337 |
Calculez l'écart moyen, la variance et l'écart type.
|
xi |
ni |
Ci |
niCi |
|Ci-X| |
ni|Ci-X| |
(Ci-X)2 |
ni(Ci-X)2 |
|
[1; 2[ |
258 |
1,5 |
387 |
3,14 |
810,12 |
9,85 |
2541,3 |
|
[2; 4[ |
133 |
3 |
399 |
1,64 |
218,12 |
2,68 |
356,44 |
|
[4; 5[ |
164 |
4,5 |
738 |
0,14 |
22,96 |
0,01 |
1,64 |
|
[5; 6[ |
108 |
5,5 |
594 |
0,86 |
92,88 |
0,73 |
78,84 |
|
[6; 9[ |
337 |
7,5 |
2527,5 |
2,86 |
263,82 |
817 |
2753,29 |
|
Total |
1000 |
4645,5 |
2107,9 |
5731,51 |